Máximo número de aristas en digrafo de diametro D

En un grafo normal, las aristas son bidireccionales, pero hoy vamos a trabajar los grafos dirigidos o digrafos, donde cada arista va acompañada de una flecha que indica la única dirección posible que se puede tomar. Así, el número de aristas en un digrafo dirigido será el doble que en el mismo normal, por lo que:

Para simplificar los siguientes dibujos (todos de digrafos), asumiremos que las aristas sin flecha son bidireccionales, valen por dos, y las dibujadas con flecha indicarán la única dirección posible. De ese modo, los dos siguientes grafos dirigidos son equivalentes.

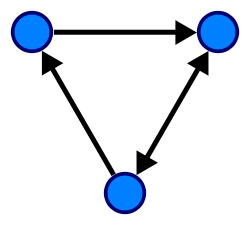
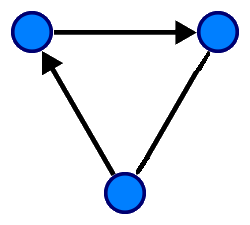
El número de nodos que hay que atravesar para ir de uno a otro se llama distancia. Si medimos la distancia de cada nodo a todos los demás y tomamos el valor máximo, tenemos el diámetro del grafo. En un grafo completo, el diámetro siempre es 1. En el las imágenes de encima, el diámetro es 2.

¿Cuál es el número máximo de aristas que puede tener un digrafo de diámetro D?

A estos grafos les llamaremos , donde n es el número de nodos y d el diámetro. Así es el grafo de diámetro 3 y 6 nodos con el mayor número de aristas posibles entre ellos. Además, utilizaremos la función para contar el número de aristas en el grafo G.

Voy a poner los ejemplos con , pero para seguir mejor los resultados, estaría bien que antes de continuar cogieras papel y lápiz y tratases de solucionar los grafos con 3 y 4 nodos, que son muy sencillos: ,

, es el caso trivial, por lo que .

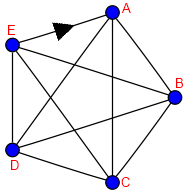
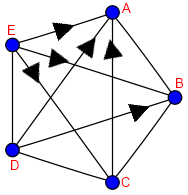
Para , simplemente tenemos que tomar , y eliminar cualquier arista en una dirección, dejándola en la otra. En la siguiente imagen se puede ver que para ir de A a E hemos de pasar obligatoriamente por otro nodo, teniendo así el diametro igual a dos que necesitábamos. Así pues, .

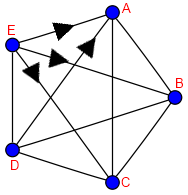
La estrategia a partir de ahora es clara, «aislar» dos nodos de forma que en una dirección siempre sea necesario recorrer los suficientes como para justificar el diámetro. La otra dirección no hay que «cerrarla», ya que únicamente hacen falta un par de nodos con distancia igual a diametro, y el resto son aristas extra que se suman a la cuenta.

Con , hemos visto que los recorridos posibles para llegar de A a E eran pasando por B, C ó D, sin embargo ahora necesitamos un salto más. Para ello, «cerramos» todas las entradas a E, salvo por D. Ahora simplemente prohibimos a A moverse directamente a D, teniendo que ir a través de B ó C. Así, al total de aristas le hemos quitado cuatro, quedando: . También podemos decir que a le quitamos tres aristas.

Repetimos el mismo proceso para , que es el último para cinco nodos y donde lo que finalmente hemos conseguido es que de A a E sólo se pueda ir por el camino ABCDE. Para ello simplemente hemos tenido que quitarle dos aristas a E(K_5^3) .

termina aquí, pero si hacemos esto con grafos mayores veremos claramente un patrón que se repite: (los paréntesis no son necesarios, sólo para visualizarlo más claro).

En realidad, es y no se puede tratar con la misma ecuación genérica que el resto, por lo que sólo funciona para .

Por otro lado, el caso específico se puede solucionar mediante otra aproximación, de igual forma para todos los grafos. Primero, sabemos que la solución constará de un único camino bidireccional que recorra todos los nodos (lo cual es además un camino hamiltoniano). Esto es . El número de aristas es n-1, que valen doble porque son bidireccionales. Veamos el ejemplo con cinco y seis nodos.

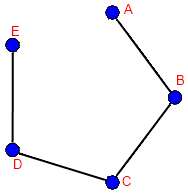
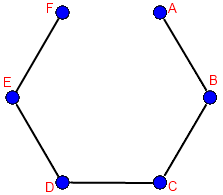
Ahora simplemente tenemos que rellenar los huecos del grafo con aristas en la dirección correcta. ¿Cuántas son? Pues fácil, el total de aristas de K_n menos n-1, que son las que acabamos de pintar.

Lo cual, se lo sumamos a lo que ya teníamos y queda:

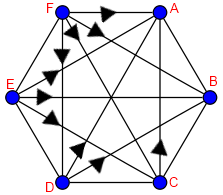
Si tomamos el caso general y sustituimos d=n-1, veremos que llegamos exactamente a la función . Si bien dije previamente que no funciona para d=1, esta nueva ecuación sí que respeta ese caso. Si despejamos n en sale una ecuación de segundo grado con raíces en 1 y 2; nos nos interesa la segunda puesto que estábamos considerando d=n-1 y demuestra que la igualdad es correcta. También es mucho más sencillo directamente sustituir n=2 en ambas fórmulas y ver que el resultado es el mismo, 2. El cual es exactamente el número de aristas en un digrafo de dos nodos y diámetro uno.

También podemos tomar valores específicos y comprobar que obtenemos el mismo resultado, por ejemplo:

¿Aplicaciones prácticas de este resultado?

En la asignatura Distributed System estamos estudiando algoritmos para seleccionar el nodo líder de una red, figura necesaria en muchas ocasiones para coordinar algoritmos distribuidos. Cada nodo tiene un identificador distinto del resto, así que la selección del líder se puede hacer bien con el que tenga el mayor ID o el que tenga el menor (para lo cual éste ha de pasar por todos los nodos).

Existen muy diversos algoritmos para comunicar el ID entre los participantes, difiriendo todos ellos en el número de rondas necesarias y de mensajes enviados. Es una asignatura a nivel teórico en la que tenemos que analizar la complejidad temporal y computacional (número de mensajes), distinguiendo mejor caso, peor, y comportamiento medio.

Un algoritmo muy simple es FloodMax, en el cual la complejidad es linear. Dura tantas rondas como el diámetro de la red, y en cada ronda cada nodo envía a todos sus vecinos el máximo valor ID que ha recibido hasta entonces. Así pues, el número de mensajes es simplemente el número de aristas por el diámetro.

Un par de clases después de esto, estaba lo suficientemente aburrido como para pensar en el peor caso de una red de tamaño N, para lo cual el primer paso era saber el máximo número de aristas posibles con cada diámetro existente.

Entonces, para saber el número de mensajes en una red de n nodos con diametro d, se hace y listo. He hecho un pequeño programita para calcular y mostrar estos valores (Graph.java y Graph.class). Ejecutando «java Graph -v N» imprime información detallada de cada diámetro, y con «java Graph N» escribe sólo los resultados para los cuales el número de mensajes es el mayor.

En realidad, la guinda del pastel sería resolver el problema de optimización para maximizar el valor msg = d \cdot E(K_n^d) \quad \forall d, 1 \le d < n[/latex] pero hasta ahí ya no llego. Consulté ayer a un amigo matemático que finalmente demostró que el máximo valor es siempre en [latex]E(K_n^{n-1})[/latex] y pese a que me indicó algunos de los pasos, no he sido capaz de reproducirlos. Si alguien se anima, [latex]\LaTeX[/latex] está activado también en los comentarios, utilizando $ latex fórmula $ , sin espacio entre «$» y «latex«.